 A rectangular enclosure with one partition is to be bounded by a wall and 30 m of fencing, as shown in the diagram. What should the dimensions be to form a rectangle whose area is 48 m2
A rectangular enclosure with one partition is to be bounded by a wall and 30 m of fencing, as shown in the diagram. What should the dimensions be to form a rectangle whose area is 48 m2 
Mrs. Napholtz's Math Site
Rectangle Problems
If the side of a square is increased by 3 m, its area is 121 m2. Find the length of a side of the original square.
(s + 3)2 = 121
s2 + 6s + 9 = 121
s2 + 6s - 112 = 0
(s + 14)(s - 8) = 0
s = 8 is the only reasonable answer.
The length of a rectangular table is 5 in. more than twice its width. Its area is 1950 in2. Find its dimensions.
Let w = width.
Length = 2w + 5
w(2w + 5) = 1950
2w2 + 5w - 1950 = 0
(2w + 65)(w - 30) = 0
w = 30 is the only reasonable solution.
ANS: 30 by 65.
The diagonal of a rectangle is 25 cm, and the length is 24 cm. Find the width of the rectangle.
Using the Pythagorean Theorem we get:
l2 + w2 = diag2
242 + w2 = 252
576 + w2 = 625
w2 = 49
w = 7
A photograph is 12 cm longer than it is wide. It is mounted in a frame 5 cm wide. The area of the frame is 620 cm 2. Find the dimensions of the photo.
| Length | Width | Area |
Photo | n + 12 | n | n2+ 12n |
Photo plus frame | n + 22 | n + 10 | n2 + 32n + 220 |
Area of the frame = 620.
n2 + 32n + 220 - (n2+ 12n) = 620
n2 +32n + 220 - n2 - 12n = 620
32n + 220 - 12n = 620
20n + 220 = 620
20n = 400
n = 20
Answer: The dimensions of the photo are 20 by 32.
The side of a square has length s. The length of a rectangle is 4 m more than the side of the square and the width of the rectangle is 2 m less than the side of the square. The perimeter of the rectangle is 24 m less than twice the perimeter of the square. Find the dimensions of each figure.
| Length | Width | Perimeter |
Square | n | n | 4n |
Rectangle | n + 4 | n - 2 | 4n + 4 |
The perimeter of the rectangle is 24 less than twice the perimeter of the square.
4n + 4 = 2(4n) - 24
4n + 4 = 8n - 24
4n + 28 = 8n
28 = 4n
n = 7
Answer: The square is 7 by 7. The rectangle is 11 by 5.
The length of a rectangle is 1 cm less than three times the width. If the area of the rectangle is
44 cm2, find the dimensions.
Width = w
Length = 3w - 1
Area = 44
w(3w - 1) = 44
3w2 - w = 44
3w2 - w - 44 = 0
(3w + 11)(w - 4) = 0
3w + 11 = 0 OR w - 4 = 0
w = -11/3 NOT A VALID DIMENSION OR w = 4.
Answer: Width = 4, Length = 11
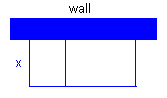
 A rectangular enclosure with one partition is to be bounded by a wall and 30 m of fencing, as shown in the diagram. What should the dimensions be to form a rectangle whose area is 48 m2
A rectangular enclosure with one partition is to be bounded by a wall and 30 m of fencing, as shown in the diagram. What should the dimensions be to form a rectangle whose area is 48 m2
The fence consists of 4 parts: 3 parallel sections, each of length x, and 1 section, parallel to the wall, whose length must be 30 - 3x.
The dimensions of the enclosure are: width = x, length = 30 - 3x.
Area = 48.
x(30 - 3x) = 48
30x - 3x2 = 48 Add 3x2 and subtract 30x
0 = 3x2 - 30x + 48 Factor out 3.
0 = 3(x2 - 10x + 16)
0 = 3(x - 2)(x - 8)
x - 2 = 0 OR x = 8 = 0.
x = 2 OR x = 8.
If x = 2, then length = 30 - 3(2) = 24. Answer: 2 by 24
If x = 8, then length = 30 - 3(8) = 6. Answer: 8 by 6.
Both are valid configurations.
The length of a rectangle is 6 m more than twice the width. If the area of the rectangle is 140 m2, find the dimensions.
The dimensions of the rectangle are w and 2w + 6.
Area = 140.
w(2w + 6) = 140
2w2 + 6w = 140
2w2 + 6w - 140 = 0
2(w2 + 3w - 70 = 0
2(w + 10)(w - 7) = 0
w + 10 = 0 OR w - 7 = 0
w = -10 Not a valid dimension. OR w = 7.
Answer: width = 7 and length = 2(7) + 6 = 20.
A rectangular pool is 8 m longer than it is wide. A walkway 2 m wide surrounds the pool. What are the dimensions of the pool if the area of the walkway is 176 m2?
| Length | Width | Area |
Pool | n + 8 | n | n2+ 8n |
Pool and Walkway | n + 12 | n + 4 | n2 + 16n + 96 |
Area of the walkway = 176.
n2 + 16n + 96 - (n2+ 8n) = 176
n2 + 16n + 96 - n2 - 8n = 176
16n + 96 - 8n = 176
8n + 96 = 176
8n = 80
n = 10
Answer: The dimensions of the pool are 10 by 18.
A rectangular garden plot is 10 m longer than it is wide. If the length is increased by 1 m and the width decreased by 2 m, the area is decreased by 42 m2. What are the original dimensions?
The new area is 42 less than the old area.
(w + 11)(w - 2) = w(w + 10) - 42
w2 -2w + 11w - 22 = w2 + 10w - 42
9w - 22 = 10w - 42 Add -10w
-w - 22 = -42 Add 22
-w = -20
w = 20
Answer: The original dimensions were 20 by 30
A poster is 25 cm taller than it is wide. It is mounted on a piece of cardboard so that there is a 5 cm border on all sides. If the area of the border alone is 1350 cm2, what are the dimensions of the poster?
Outer Area - Inner Area = Border = 1350
(x + 35)(x + 10) - x(x + 25) = 1350
x2 + 45x + 350 - x2 - 25x = 1350
20x + 350 = 1350
20x = 1000
x = 50
ANSWER: 50 by 75
A rectangle is twice as long as it is wide. If its length and width are both decreased by 4 cm, its area is decreased by 164 cm2. Find its original dimensions.
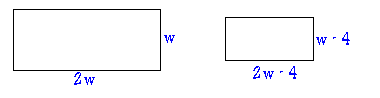
The new area is 164 less than the old area.
(2w - 4)(w - 4) = 2w2 - 164
2w2 - 8w - 4w + 16 = 2w2 - 164
-12w + 16 = -164 Add -16
-12w = -180
w = 15
Answer: Original dimensions: 15 cm by 30 cm.
A rectangle is three times as long as it is wide. If its length and width are both increased by 3 m, its area is increased by 81 m2. Find its original dimensions.
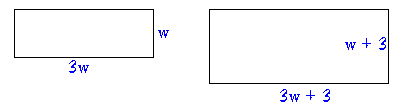
The new area is 81 more than the old area.
(3w + 3)(w + 3) = 3w2 + 81
3w2 + 9w + 3w + 9 = 3w2 + 81
12w + 9 = 81 Add -9
12w = 72
w = 6
Answer: Original dimensions: 6 m by 18 m.
A rectangle is 8 cm longer than it is wide. If its length and width are both increased by 2 cm, its area is increased by 68 cm2. Find its original dimensions.
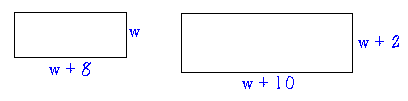
The new area is 68 more than the old area.
(w + 10)(w + 2) = w2 + 8w + 68
w2 + 2w + 10w + 20 = w2 + 8w + 68
12w + 20 = 8w + 68 Add - 8w
4w + 20 = 68
4w = 48
w = 12
Answer: Original dimensions: 12 cm by 20 cm.
A carpenter builds two decks with the same area. One deck is a square and the other is a rectangle which is 4 m longer than the square but 3 m less wide than the square. What is the area of each deck?
| Length | Width | Area |
Square | n | n | n2 |
Rectangle | n + 4 | n - 3 | n2 + n - 12 |
Since the areas are equal, we get
n2 = n2 + n - 12
0 = n - 12
12 = n
Answer:
Area of square deck = 122 = 144 m2
Area of rectangular deck = (12 + 4)(12 - 3) = (16)(9) = 144 m2