2x + y = -1
x + 2y = 4
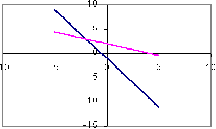 From this image, you should be able to check your own graph. The point of intersection has coordinates (-2, 3).
From this image, you should be able to check your own graph. The point of intersection has coordinates (-2, 3). Check in each of the equations:

Mrs. Napholtz's Math Site
Line and Function Problems
Solve the following system of equations graphically and check:
2x + y = -1
x + 2y = 4
 From this image, you should be able to check your own graph. The point of intersection has coordinates (-2, 3).
From this image, you should be able to check your own graph. The point of intersection has coordinates (-2, 3).
Check in each of the equations:
2(-2) + (3) = -1 Note that this will "check".
(-2) + 2(3) = 4 Note that this also "checks".
Draw the graph of y = x2 - 4x + 3 for all x: -1 < x < 5
Then:
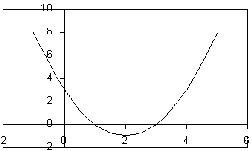
Draw the graph of the equation y = x2 - 6x + 6 for all x in the interval 0 < x < 6
On the same axes, draw the graph of x + y = 6
Using the graphs, determine the solution(s) of the system:
y = x2 - 6x + 6
x + y = 6
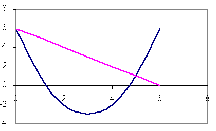
Check your graphs against this picture. The solutions are (0, 6) and (5, 1). Check these coordinates in each equation.
Write an equation in standard form of the line passing through (1, -1) with slope -4.
y = -4x + b
-1 = -4(1) + b
-1 = -4 + b
3 = b
y = -4x + 3
ANS: 4x + y = 3
Write an equation in standard form of the line passing through (2, -5) and (-4, 7).
m = (7 - -5)/(-4 - 2)
m = 12/-6
m = -2
y = -2x + b I'll use the point (-4, 7)
7 = -2(-4) + b
7 = 8 + b
-1 = b
y = -2x - 1
ANS: 2x + y = -1
Write an equation in slope-intercept form of the line passing (3,5) and perpendicular to the line whose equation is 3x - y = 5.
Given line has slope = -3/-1 = 3
Slope of perpendicular = -1/3
y = (-1/3)x + b
5 = (-1/3)(3) + b
5 = -1 + b
6 = b
ANS: y = (-1/3)x + 6
Let g(x) = x2 - 3 for the domain {1, 2, 3, 4, 5}
RANGE = {-2, 1, 6, 13, 22}
If g(x) = 22, then x = 5
g(3) = 6
A spring is hanging from a support. The distance that the spring is stretched is directly proportional to the mass attached to it. A mass of 35 g stretches the spring 10 cm. How far will a mass of 42 g stretch the spring?
Set up a proportion:
35 = 42
10
35n = 420
n=12 cm
The frequency of a vibrating string is inversely proportional to its length. If a string 30 cm long has a frequency of 40 Hz, what is the frequency of a string 24 cm long?
Products are equal:
(30)(40) = (24)(n)
n = 50