Mrs. Napholtz's Math Site
Max / Min Problems
1. An open rectangular box is to be made from a piece of cardboard 8 in. wide and 15 in. long by cutting a square from each corner and bending up the sides. Find the dimensions of the box of largest volume.
If you cut out an x by x square from each corner, and fold up the "flaps", the dimensions of the base of the box will be (15 - 2x) by (8 - 2x), and the height will be x.
The quantity we wish to "maximize" is the volume of the box, which is given by:
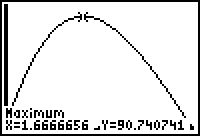
V = x(15 - 2x)(8 - 2x)
On the TI-83 Plus, set y1 = x(15 - 2x)(8 - 2x)
THINK!!! What would be a good window for this problem?
For one thing, x > 0. We also know that x must be less than 4. [Think: Can you cut out two squares of side larger than 4 if one side of the original rectangle is only 8????????]
How about values for y?
Let's see what the volume would be for x = 2:
V = 2*(15 - 2(2))(8 - 2(2)) = 88
So now we know that 100 might be a good value for y max.
| Set the Window: | Calculate the Maximum: | |
| x min | 0 |  |
| x max | 4 | |
| x scl | 1 | |
| y min | 0 | |
| y max | 100 | |
| y scl | 1 | |
The "Real" answer: x = 5/3. Volume = 90 20/27.
2. 
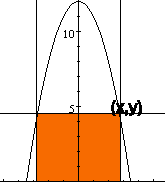Find the area of the largest rectangle with lower base on the x-axis and upper vertices on the curve y = 12 - x2.
Looking at the sketch of the curve, with a sample rectangle, we can deduce:
Length of rectangle = 2x.
Height of rectangle = y.
The quantity we wish to "maximize" is the area of the rectangle, which is given by:
A = 2x(y)
B U T: y = 12 - x2.
Therefore, A = 2x(12 - x2).
On the TI-83 Plus, set y1 = 2x(12 - x2)
Please be aware that the "y" on the TI-83 Plus is the AREA of the rectangle, and bears no relation to the y - coordinate on the parabola sketched above!
THINK!!! What would be a good window for this problem?
From the sketch, we see that 0 < x < SQRT(12) [THINK!].
How about values for y?
Let's see what the area would be for x = 2:
A = 2*(2)(12 - 22) = 32
So now we know that 50 might be a good value for y max.
| Set the Window: | Calculate the Maximum: | |
| x min | 0 |  |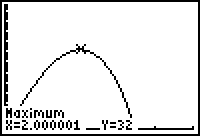
| x max | 5 | |
| x scl | 1 | |
| y min | 0 | |
| y max | 50 | |
| y scl | 1 | |
The "Real" answer: x = 2. Area = 32.
3. 
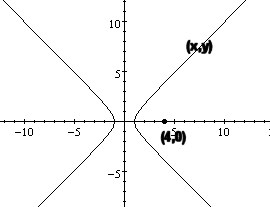Find the points on the curve x2 - y2 = 1 that are nearest the point (4, 0).
Looking at the sketch of the curve, we can deduce that there will be two answers, one in the first quadrant (marked as (x,y)), and a "matching" answer in the fourth quadrant.
We will find the point in the first quadrant.
The quantity we wish to "minimize" is the distance between (x,y) and (4,0), which is given by:
D = SQRT((x - 4)2 + (y - 0)2)
= SQRT((x - 4)2 + y2)
B U T: y2 = x2 - 1. [Rearrange the terms of the original equation!]
Therefore
D = SQRT((x - 4)2 + x2 - 1)
On the TI-83 Plus, set y1 = SQRT((x - 4)2 + x2 - 1)
THINK!!! What would be a good window for this problem?
From the sketch, we see that 0 < x < 10 might be reasonable.
How about values for y?
Again, from the sketch, we see that 0 < y < 10 might also be reasonable.
| Set the Window: | Calculate the Maximum: | |
| x min | 0 |  |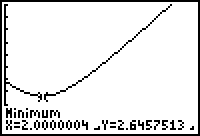
| x max | 10 | |
| x scl | 1 | |
| y min | 0 | |
| y max | 10 | |
| y scl | 1 | |
Again, remember that the "y" on the calculator is the DISTANCE, not the y-coordinate of the answer!!
The "Real" answer: (2,SQRT(3)) and (2,-SQRT(3)). Distance = SQRT(7).
4. Find two positive numbers whose sum is 4 and such that the sum of the cube of the first and the square of the second is as small as possible.
Let the two numbers be represented by x and (4 - x).
Then the quantity we are to minimize is: x3 + (4 - x)2.
THINK!!! What would be a good window for this problem?
From the problem, we can deduce that 0 < x <4 is reasonable.
How about values for y?
Pick a value for x -- try x = 3.
Then x3 + (4 - x)2 = 27 + 1 = 28.
So we can try 0 < y < 50
| Set the Window: | Calculate the Maximum: | |
| x min | 0 |  |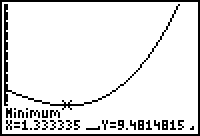
| x max | 4 | |
| x scl | 1 | |
| y min | 0 | |
| y max | 50 | |
| y scl | 1 | |
Again, remember that the "y" on the calculator is x3 + (4 - x)2!!
The "Real" answer: The numbers are: 4/3 and 8/3, and the sum of the first one cubed and the second one squared = 256/27.
5. 
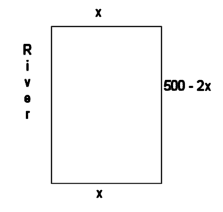One side of an open field is bounded by a straight river. How would you put a fence around the other three sides of a rectangular plot in order to enclose as great an area as possible with 500 feet of fencing?
We would like to maximize the area, which is given by A = x(500 - 2x). Enter this for y1 in the calculator.
THINK!!! What would be a good window for this problem?
x between 0 and 250 might be reasonble.
How about values for y?
Pick a value for x -- try x = 150.
Then Area = 150(500 - 2(150)) = 30,000.
So we see that we will have to allow for very large y.
| Set the Window: | Calculate the Maximum: | |
| x min | 0 |  |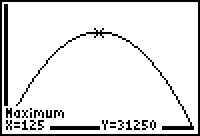
| x max | 250 | |
| x scl | 1 | |
| y min | 0 | |
| y max | 40,000 | |
| y scl | 1 | |
Again, remember that the "y" on the calculator is the area of the region.
The "Real" answer: width = 125, length = 250, with maximum area of 31,250.